En tiempos de incertidumbre, la Teoría de juegos no es sólo un juego matemático: es la aplicación del pensamiento estratégico a la toma de decisiones.

Ante una situación de incertidumbre ¿qué debemos hacer? Cuando los resultados dependen no sólo de nuestras decisiones, sino también de lo que decidan los otros (los concurrentes) ¿cómo decidir? Cuando los factores a tomar en cuenta por nosotros y por los demás concurrentes no son sólo racionales, sino también emocionales o hasta psicológicos ¿cómo tomar una decisión? Una herramienta útil son los postulados de la Teoría de juegos.
La Teoría de juegos, ortodoxamente definida,1 es la «rama de las matemáticas aplicadas que proporciona herramientas para analizar situaciones en las que las partes, llamadas jugadores, toman decisiones que son interdependientes. Esta interdependencia hace que cada jugador considere las posibles decisiones o estrategias del otro jugador al formular su propia estrategia. Una solución para un juego describe las decisiones óptimas de los jugadores –que pueden tener intereses similares, opuestos o mixtos– y los resultados que pueden resultar de estas decisiones».

Originalmente la Teoría de juegos fue utilizada para analizar los juegos de salón, sin embargo sus aplicaciones son mucho más amplias. Esta teoría fue desarrollada por John von Neumann y su colega en la Universidad de Princeton, Oskar Morgenstern (ver cuadro 1). Lo hicieron para tratar de resolver problemas económicos, su obra de referencia precisamente se intitula así: Theory of Games and Economic Behavior, en español: La Teoría de los juegos y del comportamiento económico.2

Muy posiblemente, su principal aportación es la observación que hacen acerca de la economía: para ellos es muy similar a un juego, donde los jugadores tratan de anticiparse a las «jugadas» (movimientos) de los demás y por lo tanto las matemáticas tradicionales, que se utilizaban para las ciencias físicas, resultaban muy limitadas, para ellos se requería un nuevo tipo de matemáticas, al que llamaron Teoría de juegos. Para algunos, el nombre es poco apropiado pues no comparte la diversión o la frivolidad asociada a los juegos.

Una manera de entenderlo es con la metáfora de una obra de teatro: El Juego que todos jugamos (1970) original de Alejandro Jodorowsky (nacido en Chile en 1928, residente en México y Francia). La comparación es buena, pues en la obra el autor presenta la realidad que enfrentamos; realidad que cada individuo diagnóstica y vive de manera diferente, poniendo en su manera de «jugar» (de enfrentarla) sus ambiciones, sus temores, sus anhelos, sus gustos, sus debilidades y su propio aprendizaje. Se trata de una alegoría que nos muestra lo que queremos expresar en este artículo: las situaciones que enfrentamos se asemejan a juegos, donde cada jugador no actúa únicamente de manera racional.

Para Von Neumann y Morgenstern: «un juego es una situación conflictiva en la que uno debe tomar una decisión sabiendo que los demás también toman decisiones, y que el resultado del conflicto se determina, de algún modo, a partir de todas las decisiones realizadas».

DEL PÓKER A LA ECONOMÍA
Von Neumann, uno de los matemáticos más importantes de la edad moderna, se entretenía observando e investigando las estructuras matemáticas del póker, el ajedrez y los dados (él era aficionado al póker), así como de otros juegos. Conforme lo iba haciendo, se dio cuenta de que los teoremas (hipótesis) que iba esbozando podían aplicarse a temas de economía y política. Estas ideas fueron las que plasmó en la obra mencionada, con su colega Morgenstern. Ambos pensaron solamente en los alcances o aplicaciones de esta teoría para la economía, pero su obra fue rápidamente utilizada no sólo por economistas, sino por investigadores de ciencias sociales y estrategas militares. Su planteamiento inicial es muy sólido y a partir de esa base se ha ido desarrollando.

A lo largo de los años, la Teoría de juegos se ha aplicado a una gran diversidad de situaciones, donde las decisiones de cada jugador (considerando sus propias decisiones y las del resto de los jugadores) definen el resultado. También hace hincapié en los aspectos estratégicos de la toma de decisiones: los objetivos que desean lograr los jugadores, los recursos con que cuentan para lograrlos y el plan de acción o pasos para hacerlo, es decir, para «jugar». Se observa entonces que los resultados no se dan por pura casualidad, con lo que la Teoría de juegos va más allá de la Teoría de la probabilidad (procurando complementarla). Además, permite prepararse para enfrentar situaciones de incertidumbre.

Uno de sus usos, por ejemplo, es determinar cómo actúan las empresas para establecer el precio óptimo de venta de productos o servicios de cara a sus contrincantes en el mercado. También se utiliza en situaciones políticas (elecciones mediante votación) para ver cómo se comportaran los votantes (individualmente o en grupo, sea alrededor de un partido político, sea en torno a una coalición). Sirve también para ubicar un recurso, por ejemplo para seleccionar el mejor lugar para construir una fábrica, y en el ámbito biológico ayuda a explicar el comportamiento de plantas y animales en su eterna lucha por la supervivencia.

El hecho de que la Teoría de juegos aborde situaciones tan diferentes y numerosas nos ayuda a entender que no existe una sola Teoría de juegos. A partir del libro de Von Neumann y Morgenstern se han propuesto varias teorías, cada una de ellas aplicable a distintas situaciones, con sus propias limitaciones o restricciones. Éstas tratan de explicar un juego en particular y cómo se «juega» para llegar a una solución o resultado.

Podría pensarse que la Teoría de juegos sería una especialidad de la Psicología3 en vez de ser una especialidad de las matemáticas pero no es así, pues supone en primer lugar que los jugadores son razonables. Ante esta propuesta (jugar «estratégicamente»), lo que pretenden Von Neumann y Morgenstern es poder contestar si existe una manera racional de jugar, especialmente en aquellos casos donde los contrincantes pueden alardear o tener segundas intenciones (existe incertidumbre). Podría entonces pensarse que debe haber una manera racional de jugar cualquier juego per se. «¿Es así?», se preguntaron nuestros autores, pues el mundo no está regido solo por la lógica: en muchas decisiones de nuestra vida diaria abunda lo irracional.

UNO PARTE Y OTRO ESCOGE 
Para entender de manera muy simple la Teoría de juegos, pensemos en una madre que debe repartir un pedazo de pastel para dos hermanos. Si lo hace ella, podrán acabar peleándose por pensar ambos que una mitad es mayor que la otra. Al pedir que uno parta y otro escoja, el que parte será especialmente justo, pues sabe que el otro tomará siempre la que le parezca mayor. En el mundo de los negocios, lo hemos visto, cuando dos socios de una empresa deciden separarse: aquí el mecanismo o la estrategia es «tú ponle precio, yo decido si te compro o si te vendo». Es el mismo principio: utilizar una manera racional de jugar, sabiendo que el otro podrá tener «segundas intenciones». Se trata de un juego (conflicto) de intereses encontrados y su solución pasa por una decisión muy racional.

CATALOGANDO LOS JUEGOS
Los juegos pueden clasificarse según diversas características, por ejemplo, la cantidad de jugadores. Hay entonces juegos de una persona, dos personas o de «n» personas (siendo «n» más de dos). Consideremos también que un jugador no necesita ser un individuo; puede ser un equipo de trabajo, una empresa, un país o un equipo compuesto por varios integrantes con intereses compartidos.

Hay juegos de información perfecta, como el ajedrez, donde cada jugador sabe todo sobre el juego en todo momento. Y hay juegos de información imperfecta, como el póker, porque los jugadores no conocen todas las cartas de sus oponentes.

Los juegos de una persona se conocen también como juegos contra la naturaleza. Como el jugador carece de oponentes, sólo necesita identificar las opciones disponibles para elegir la «jugada» que, según él, le dará el resultado óptimo. Como se manejan probabilidades, podría parecer más complicado, pero en principio la decisión es relativamente simple. Por ejemplo, una persona que, para salir, decide llevar o no un paraguas, pondera los costos y beneficios de llevarlo o no. Puede tomar una decisión equivocada, pero no existe un oponente consciente. Es decir, se supone que la naturaleza es completamente indiferente a la decisión del jugador y la persona basa su decisión en probabilidades simples (de que llueva). Enumeraremos algunos juegos y algunos de los principios subyacentes a los mismos.

EL DILEMA DEL PRISIONERO
Es uno de los problemas fundamentales de la Teoría de juegos: nos muestra que dos personas pueden no cooperar entre ellas, incluso si les beneficia.
Su enunciación es la siguiente: La policía arresta a dos sospechosos. No hay pruebas suficientes para condenarlos y son encarcelados aisladamente, es decir, no tienen contacto con su compañero. El policía a cargo los visita a cada uno y les hace la misma oferta: si uno delata y su cómplice no, el cómplice será condenado a la pena total (10 años) y quien delata será liberado. Si uno calla y el cómplice delata, el primero recibirá esa pena (10 años) y será el cómplice quien salga libre. Si ambos delatan, ambos serán condenados a cinco años. Si ambos lo niegan, todo lo que podrán hacer será encerrarlos durante un año por un cargo menor. (Ver cuadro 1 para comprender el dilema).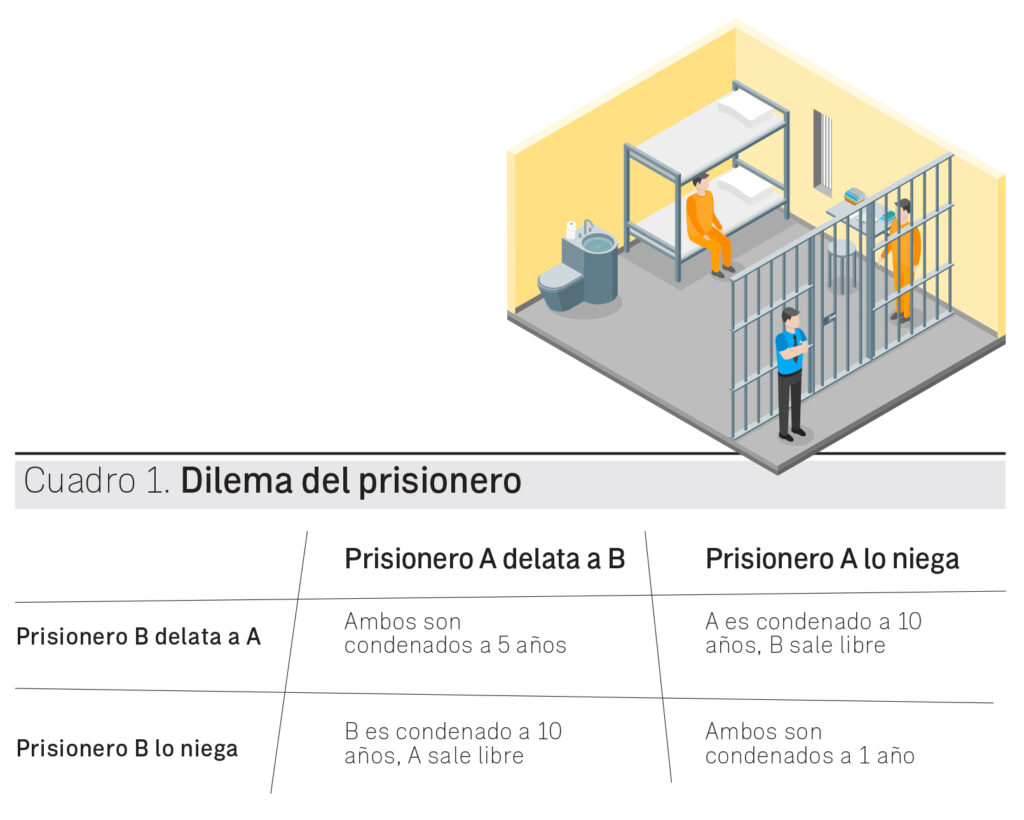

Nobel de economía en 1994. Parte de su fama se debe a la película A Beautiful Mind (Mente brillante) basada en su vida, protagonizada por Russell Crow.
El equilibrio de Nash podría considerarse una variación del dilema del prisionero; se enuncia de la siguiente manera: «Situación donde cada participante en el mercado cree que está tomando las mejores decisiones y que cada otro participante está haciendo lo mismo». El equilibrio estabiliza las expectativas, valida las decisiones y refuerza las conductas de los participantes.

Nash ofrece un concepto de solución para juegos con dos o más jugadores donde, como señalamos, cada jugador conoce y ha adoptado su mejor estrategia y todos conocen las estrategias de los otros. Se crea el equilibrio porque cada jugador no gana nada modificando su estrategia, mientras los otros jugadores mantengan las suyas; es decir cada jugador está utilizando una estrategia (una manera de jugar) que maximiza sus ganancias, dadas las estrategias de los otros. Al estar en equilibrio cada jugador, de manera individual, no tiene incentivos para modificar unilateralmente su estrategia.

Al afirmar que el equilibrio estabiliza las expectativas, valida las decisiones y refuerza las conductas (de los participantes), nos damos cuenta de que se está creando un «ecosistema» donde todos están satisfechos y no quisieran cambiar; de hecho, están «controlando» la incertidumbre, de alguna manera. Un ejemplo del equilibrio de Nash podríamos encontrarlo en el sector de los teléfonos celulares inteligentes, que se conformó con el lanzamiento del iPhone en 2007 (ver figura 1).

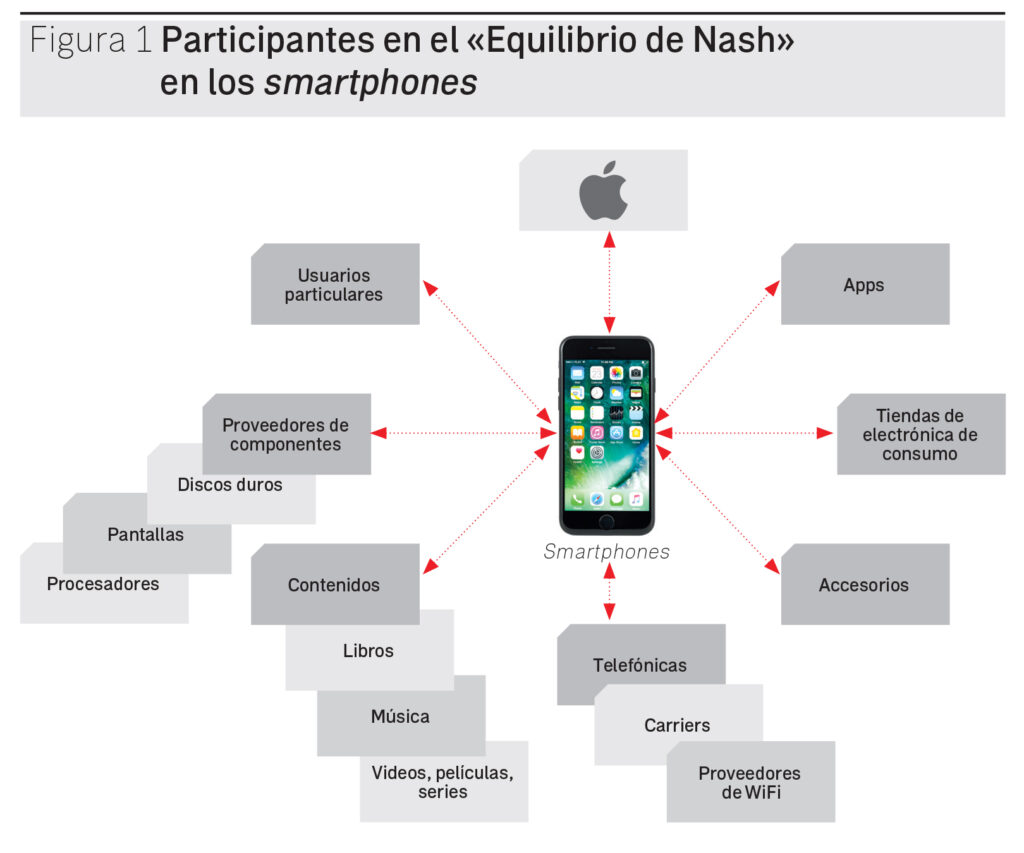
En la figura hemos incluido a todos los jugadores en el sector de los smartphones, se trata de aparatos que, más que ser solamente teléfonos, constituyen una «plataforma» con numerosas aplicaciones que facilitan la vida del usuario. Cada uno de estos «jugadores» tiene su propia estrategia y cada uno de ellos cree que está haciendo lo mejor, dadas las estrategias de los demás. Esta situación crea el «equilibrio» y si alguien quiere entrar en este sector («jugar ese juego») tendría que hacerlo siguiendo las reglas y estrategias ya establecidas, hasta que llegue alguien a «disruptir» el sector (como en su momento lo hizo Apple en 2007, al lanzar su iPhone), creando entonces otro «ecosistema».

INCERTIDUMBRE Y TEORÍA DE JUEGOS
Algunas ideas prácticas para enfrentar la incertidumbre en los negocios, utilizando la Teoría de juegos:

1.  Oligopolios. En el largo plazo, todos terminaremos compitiendo en mercados oligopólicos. Por lo tanto, el director debe entender cómo piensan los pocos competidores que llegarán al final de la lucha por dominar el mercado, porque las decisiones de ellos y las suyas están estrechamente relacionadas e interconectadas.
2. Patrones (esquemas). La Teoría de juegos ayuda a encontrar patrones de comportamiento racional para predecir y tratar de entender las posibles decisiones o jugadas que tornarán los competidores.
3. Anticipación. El análisis previo de la situación (el diagnóstico) es la piedra angular de la estrategia. La Teoría de juegos ayuda a realizar un estudio de los posibles escenarios que se pueden presentar en el corto, mediano y largo plazo.
4. Decidir. Ante momentos de gran incertidumbre en los mercados, la Teoría de juegos permite a los directores trabajar sobre posibles escenarios para tomar una decisión de mejor calidad; gestionar los «juegos» en los que se quiere competir y también elegir los «juegos» que se quieren evitar.
5. Alocentrismo. Aunque usualmente se conciben los negocios de manera egocéntrica (juegos que se centran en la postura, nada más), la Teoría de juegos tiende al alocentrismo: observar a los otros competidores para considerar y entender la interdependencia de sus acciones.
6. Beneficios y utilidades. Los negocios no son juegos donde para que uno gane los demás tienen que perder. La Teoría de juegos permite visualizar opciones donde varios competidores obtengan beneficios a la vez (ganar-ganar).
7. Empoderamiento. Cada empresa puede darle nuevas formas al juego de la competición, permitiéndole pasar de ser un agente pasivo a un agente y jugador activo, generador de cambio y hasta desarrollador de nuevos juegos (modelos) de negocio.
8. Permanente (continuo). El juego de los negocios no tiene final, se puede perder en un juego, pero de inmediato se inicia otro diferente. El juego de cambiar de negocios no tiene final, lo que obliga al director a reinventarse y pensar en gestionar juegos constantemente y de manera diferente.
9. Estructura. La toma de decisiones no debe darse a la ligera. La Teoría de juegos le permite al director ser más estructurado y prudente a la hora de encontrarse ante situaciones complejas, cuyo desarrollo conlleva la posibilidad de enormes consecuencias y de secuencias de juegos consecutivos y entrelazados en el tiempo.
10. Trascendencia. La teoría de juegos no es sólo un juego matemático: es la aplicación del pensamiento estratégico en la toma de decisiones.

LA ESTRATEGIA Y LA TEORÍA DE JUEGOS
La Teoría de juegos nos ayuda a tomar decisiones y, frente a la incertidumbre, formular la estrategia en el mundo de la empresa, basándonos no sólo en nuestro punto de vista, sino también en cómo pensamos que actuarán los demás jugadores, de acuerdo con la decisión que tomemos nosotros. Esto requiere un cuidadoso diagnóstico, que siempre es útil.

Un concepto importante: la «estrategia dominante», es la que da el mejor resultado sin importar lo que decidan los otros jugadores (por ejemplo, en el dilema del prisionero la estrategia dominante es delatar).

La Teoría de juegos no sólo es utilizada en la economía, también se usa en otros muchos ámbitos. A nosotros nos interesa el ámbito de la empresa, pero también tiene aplicaciones en la política, la estrategia militar, la biología y, por supuesto, los juegos de azar, como el póker o el blackjack.

Notas al pie

1 Definición tomada de: https://www.britannica.com/science/game-theory
2 Theory of Games and Economic Behavior, Princeton University Press, 1944, John von Neumann y Oskar Morgenstern, Princeton Nueva Jersey, Estados Unidos (un libro difícil de leer, 641 páginas llenas de fórmulas).
3 Tomamos aquí algunas ideas del artículo «Teoría de la Decisión: Contribuciones de von Neumann» de Carlota Gastaldi, Marcel Urrea y Pedro Fernández de Córdoba, publicado en Divulgaciones Matemáticas, v. 6, Nº 1 (1998), p 37-42, publicación de la Universidad del Zulia.
4 Algunas de estas ideas tienen su origen en el libro Teoría de juegos y estrategia empresarial de José David Ulloa Soto, Editorial Académica Española, España, 2015.